大学时学习的数据结构课程,只剩下零星的记忆,在工作中用到时候,对一些概念定义总是似曾相识却又不甚透彻,所以决心重新系统的学习一下数据结构与算法这门课程. 本系列文章是我在学习中国大学MOOC网中浙江大学陈越、何钦铭老师的《数据结构》这门课程的学习笔记.
数据结构
“数据结构(data structure)是计算机中存储、组织 数据的方式。”-中文维基百科
- 解决问题方法的效率,和数据的组织方式有关.
- 解决问题方法的效率,和空间的利用效率有关.
- 解决问题方法的效率,和算法的巧妙程度有关.
什么是数据结构
数据对象在计算机中的组织方式
- 逻辑结构
- 物理存储结构
数据对象必定与一系列加在其上的操作相关联
完成这些操作所用的方法就是算法
抽象数据类型(Abstract Data Type)
数据类型
- 数据对象集
- 数据集合相关联的操作集
抽象
描述数据类型的方法不依赖于具体实现 * 与存放数据的机器无关 * 与数据存储的物理结构无关 * 与实现操作的算法和编程语言无关
算法(Algorithm)
- 一个有限指令集
- 接受一些输入(有些情况不需要输入)
- 产生输出
- 一定在有限步骤后终止
- 每一条指令必须
- 有充分明确的目标,不可以有歧义
- 计算机能处理的范围之内
- 描述应不依赖于任何一种计算机语言以及具体的实现手段
空间复杂图S(n)
根据算法写成的程序在执行时占用存储单元的长度.这个长度往往与输入数据的规模有关.空间复杂度过高的算法可能导致使用的内存超限,造成程序的异常中断.
时间复杂度T(n)
根据算法写成的程序在执行时耗费时间的长度.这个长度往往与输入数据的规模有关.时间复杂度过高的低效算法可能需要很久也等不到运行结果.
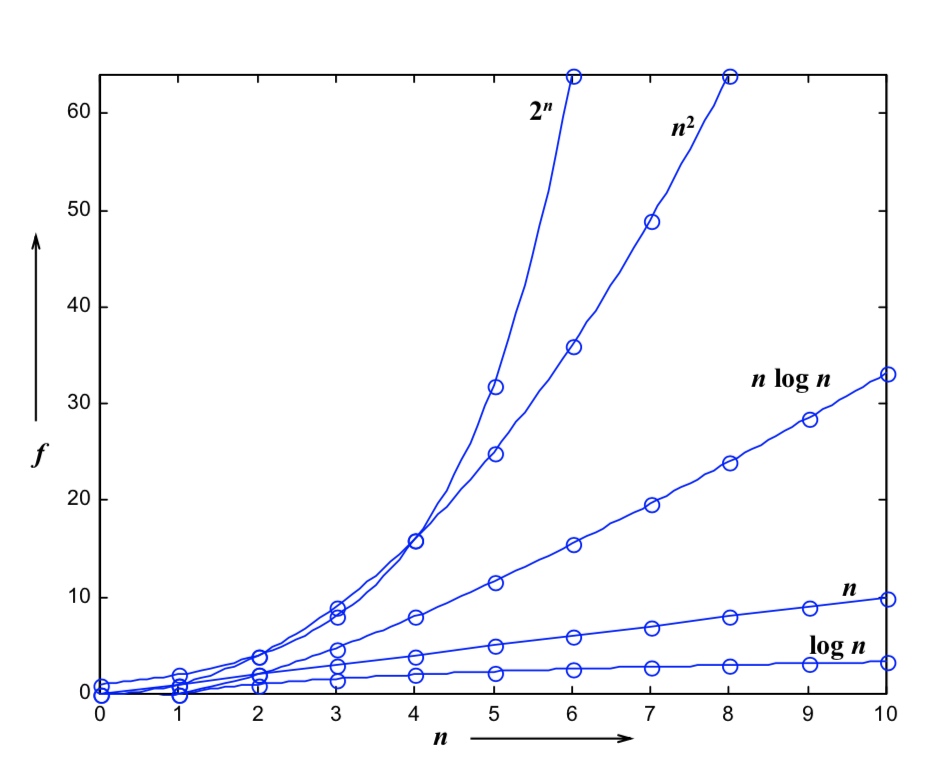
复杂度分析
- 若两段算法分别有复杂度T1(n) = O(f1(n)) 和T2(n) = O(f2(n)),则
- T1(n) + T2(n) = max( O(f1(n)), O(f2(n)) )
- T1(n) * T2(n) = O( f1(n) * f2(n) )
- 若T(n)是关于n的k阶多项式,那么T(n)=Θ(nk)
- 一个for循环的时间复杂度等于循环次数乘以循环体 代码的复杂度
- 一个for循环的时间复杂度等于循环次数乘以循环体 代码的复杂度
最大子列和问题
给定N个整数的序列{ A1, A2, …, AN},求最大连续子列的和
1 2 3 4 5 6 7 8 9 10 11 12 13 |
func SublistMaxSum(list:[Int])->Int {
var sum = 0, max = 0
for item in list {
sum += item;
if sum > max {
max = sum
}
else if sum < 0 {
sum = 0
}
}
return max
} |